Contents
Membrane time constant
Single exponential
Dual exponential
Error function
Fit failure
Multiple measurements
Averaging
Fitting Membrane Time Constant
It may be useful in neuroscience (and electrical engineering) to determine the time constant of a curve, and DataView has a specialised curve-fitting option for this purpose.
DataView can fit 3 pre-defined models:
a single exponential
$$V_t = V_{\infty} +(V_0-V_{\infty})e^{\Large{\frac{-t}{\tau_m}}}$$
a double exponential
$$V_t = V_{\infty} + w_0(V_0-V_{\infty})e^{\Large{\frac{-t}{\tau_0}}} + w_1(V_0-V_{\infty})e^{\Large{\frac{-t}{\tau_1}}}$$
and an error function:
$$V_t = V_0 + (V_{\infty} - V_0) + \mathsf{erf}\left(\sqrt{\frac{t}{\tau_m}}\right)$$
The assumption is that a pulse of current is injected into the system at time t0 when the membrane potential is V0. Then Vt is the membrane potential at time t after the start of the pulse, V$_{\infty}$ is the steady-state final potential and τ is the time constant with which it is achieved. w is the weighting within a mixture.
The single exponential fit is appropriate for a spherical cell with no dendrites or axon attached (or where all we care about is the fundamental membrane time constant). The double exponential fit is better for the Rall “ball-and-stick” neuron model of a soma, with dendrites and axon lumped into a single equivalent cylinder. In this case a “true” fit requires the weighted sum of an infinite number of exponential terms, but DataView only calculates the first 2 time constants (and assumes that w1 = 1-w0) on the basis that higher-order time constants are rarely significant. In this model, the longest time constant (t0) is equivalent to the fundamental membrane time constant, and the ratios between this and the next time constant (t1) gives information about the electrotonic length of the equivalent cylinder, while the weighting coefficients and time constants combined allow calculation of the cylinder-to-soma input impedance ratio (Rall, 1969). Details of this are beyond this tutorial. The error function fit is best for recordings made from a passive cable of infinite length and constant diameter, if you ever encounter one.
The fitting algorithm is the same as that used for general non-linear curve fitting.
- Load the file membrane tau.
This shows the voltage responses (lower trace) to a positive current pulse followed by a negative current pulse (upper trace). The recording was made in whole-cell patch configuration, and unfortunately there is 50Hz interference on the record - but this just adds to the realism of the tutorial (I hope). The two responses were recorded with discontinuous sweeps, with the sweep start marked as events in channel a. The analysis requires the onset and offset of the responses to be marked by events, which in this case have been added manually, and are located in channel b. [Note: if adding events manually, you can get high accuracy by adding onset and offset events separately with a high time-resolution fast timebase, and then merging them to get a single event.]
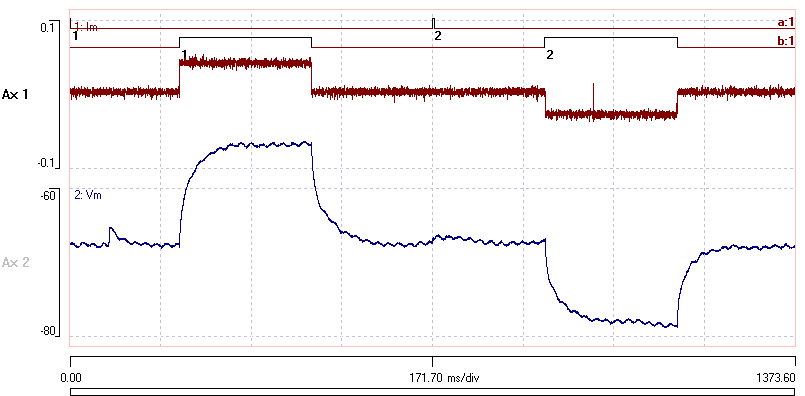
We are going to try to extract time constants from the relaxation curve following the negative current pulse (i.e. the second pulse).
- Select the Analyse: Estimate time constant re events menu command to show the Estimate membrane time constant dialog box.
The dialog box has four components; Data source view, Model and Fit panel groups on the left which set up the analysis, and two displays on the right which show the results graphically. Initially, these displays make no sense, because the default conditions are inappropriate.
First set up the Data source view.
- Set the Trace ID to 2 because this is the voltage trace. (An EPSP appears in the upper display panel – ignore this!)
- Set the Event channel to b because this is the channel that marks the current pulses.
- In the Data source view frame set the Disp width to 200.
We can see from the main display that the response to a current pulse takes about 200 ms to complete. - Set the Start ID to 2 because we are going to analyse the second pulse.
The onset response curve should now be visible in the upper panel on the right. If the data were at the wrong gain or position, we could adjust these using the standard controls in the main view. - We want to analyse the relaxation curve, so set the Start relative to event to Off time.
- Set the Start relative to event disp (ms) to -10, so that we see some of the data before the start of the relaxation.
You should now see the membrane potential relaxing from a negative current stimulus pulse. These are the data we derive the time constant from.
Single Exponential Fit
Start off by fitting a single exponential to the data.
- Click the Guess param button in the Fit frame.
In the Model frame, the Start V value is set to the first voltage value in the display, and the End V to value is set to the last voltage value in the display. Two draggable horizontal grey cursors are drawn in the upper display panel (showing the membrane potential). These are labelled V(0) and V(inf), and are drawn at voltages determined by the Start and End values. You can drag these cursors to adjust the values if necessary.
DataView makes a guess at a time constant for a single exponential decay appropriate to these values, and draws the relaxation curve according to these parameters in red superimposed on the data in the upper panel. It also sets a pair of blue cursors , which mark the region in which the curve-fitting procedure (see below) will operate.
The lower panel shows a plot of the data against time, where the data are the natural log of the relative difference between the voltage at that time (sign-adjusted according to whether the waveform is rising or falling), and the final voltage. If the data follow a single exponential time course, then they will fall on a straight line in this plot. The extent to which they deviate from a straight line indicates the extent to which the simple model fails. Superimposed on the data is a red line again showing a log plot of the relaxation curve.
The voltage trace is contaminated by interference, so to get a more accurate value for the end voltage, we should average its value over the last part of the display.
- In the Fit frame, click the Avg end check box, and enter 40 into the time to avg box. Note that a draggable purple vertical line appears some time (40 ms) before the right hand end of the V(inf) grey line.
- Click the Guess param button again.
The final voltage parameter (End V) and the data noise (Data S.D.) are now calculated from the last 40 ms of the display (hence the purple line). As can be seen, the red line looks like a reasonably close fit to the data before we even start curve fitting.
At this stage we are confident in the End V and Data S.D. parameters, since these are measured accurately from the response. So we do not want the curve fitting procedure to adjust thesevalues.
- In the Model frame at the bottom left, check the Fix boxes beside the End V and Data S.D. parameters.
Note that we are not confident in the Start V parameter because its value in the recording depends on the accuracy of the “bridge balance” setting in the recording patch amplifier that cancels the series resistance. Any inaccuracy here will affect the estimate of Time constant, so leave the Fix box unchecked beside the Start V parameter.
- The blue vertical lines on the red fit line only include quite a small part of the curve. You could drag these lines by eye, but you can set also set them explicitly. Set the Rel fit region, start value to 0 ms, and the end value to 90 ms. Note how the blue lines shift position. These indicate the regions of data that will be used during curve-fitting.
We are now ready to ask DataView to calculate a better fit time constant than its first guess.
- Click the Curve fit button.
The red line adjust through a number of iterations. If the iter done parameter reads the same as the Max iter parameter (in this case 100) it means that the fit did not reach the convergence criterion within these iterations. You can just click Curve fit again (or increase the Max iterations parameter).
At this point both the time constant and the initial voltage have been adjusted to achieve the best possible fit to the data, assuming a single exponential model. The “by eye” fit of the upper trace looks good in the later part of the curve, but it does not follow the data in the early part near the blue line, and the estimated Start V is substantially above that in the data. The RMS parameter in the Fit frame is about 1.8 and the p value is very small, suggesting that the model is not a very good fit to the data. Note the BIC value of -1051 (see the Curve fit tutorial for an explanation of what the BIC is and how to interpret it).
Double exponential fit
We will now extend the model to a double exponential.
- Select the Double exponential type in the Model frame.
Note that the lower log-plot graph has developed an additional set of data points and shows 2 red lines. When data are fitted to a multi-exponential model, one can “peel” exponentials, which means iteratively subtracting the fitted longest time constant from the data, and plotting the residuals (see the Rall paper for details). The end result is a set of data representing the next slowest time constant, and that is represented in the new dataset in the bottom graph.
- Click Curve fit. The fit rapidly reaches the convergence criterion.
If at any point you see a pop-up message saying that the fit failed to converge, this means that the fitting procedure has gone badly wrong and is heading off in the wrong direction. There are two possible solutions to this: improve the initial guesses of parameters and/or reduce the Step size of the fit procedure. However, in my trials with these settings this did not happen.
At this point, the Estimate membrane time constant dialog box should look approximately like this:
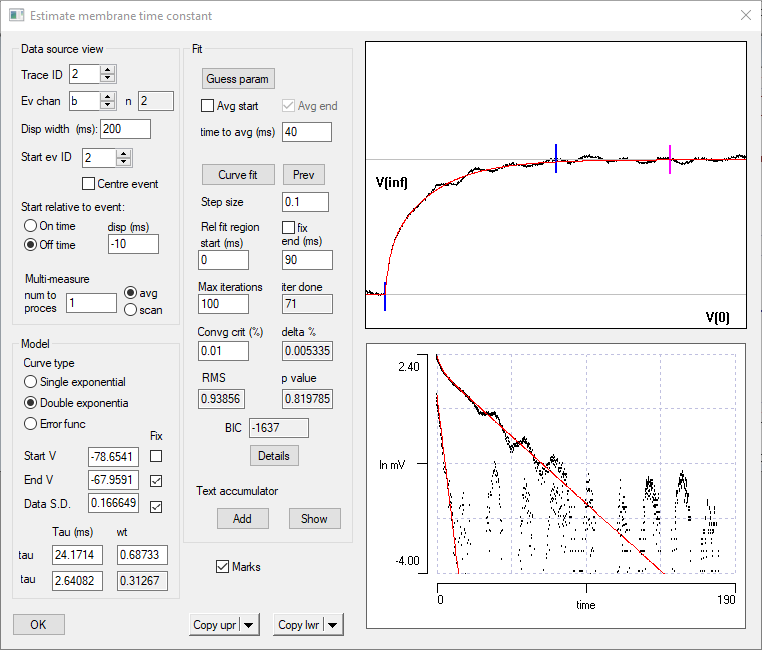
We could copy either panel to the clipboardwith the two Copy buttons.
Note that the RMS is close to 1, and the p value is not significant. Both of these are indicators that the model is a good fit to the data. Also note the BIC value of 1637, which is substantially lower than that achieved with the single exponential fit. Finally, the unconstrained fitted Start V value is a close match to the "by eye" bridge balance setting used by the original experimenter.
Error function fit
Finally, let’s try fitting the Error function.
- Select the Error function type in the Model frame.
- Click Curve fit.
There is rapid convergence to the new model, and both the RMS and p-value (as well as visual inspection) suggest that the error function also provides a good fit. However, the starting potential is lower than that in the data (which could be due to bridge imbalance), and, more importantly, the BIC value of ‑1594 is not as low as that achieved with the double exponential fit. This indicates that we should accept the more complex double-exponential model in preference to the error function model, even though it has more parameters (and certainly in preference to the single exponential model, which has much lower accuracy).
Fit fails
Sometimes the curve fit procedure goes horribly wrong, and you end up with nonsense values, such as negative time constants, or weights outside the allowed range of 0 - 1. Usually, the programme will detect this and flag a failure to converge, but sometimes it just carries on regardless. You can revert to the previous (hopefully OK) set of parameters by clicking the Prev button. You should then try to improve your initial “guess” of parameter values, or reduce the step size, or change the fit region. With luck, some combination of these changes will get things back on a sensible track. In fact, it is often surprising how close you can get to “correct” parameter values with by-eye adjustment, by closely observing the changes in the two graphical displays.
Making Multiple Measurements
If you are need to fit a number of waveforms, you can use a Text accumulator to store results.
- Set the Start event ID appropriately and carry out a fit as described above. You can try various parameter settings and options until you are happy with the quality of the fit.
- Rather than having to note down the values for each fit, click the Add button. This writes the fit values into the accumulator.
- Repeat for each desired event.
- At any stage you can display the contents of the accumulator by clicking Show. You can edit or clear values in the accumulator, and these will be retained if you dismiss the accumulator dialog with OK rather than Cancel.
Batch Fit
If you have a lot of measurements and they are all similar in their properties, you can perform a batch fit.
- Select the scan option (rather than average)
- Set the Number to process value to the number of responses you wish to average
- Click Curve fit
The programme attempts to fit each event in sequence using the current parameters (fit region and any fixed curve parameters). The outcome is stored in a text accumulator which is displayed when all events have been processed.
Averaging
If you have multiple measurements of the response to a sequence of identical current pulses, you can fit to the averaged response, rather than to each individual response.
- Make sure that average (not scan) is set as the process.
- Set the Number to process value to the number of responses you wish to average
The display now shows the average response, and you can proceed with the fit as described above.